Science
-
To the stars with Gear VR!
Getting more serious about VR… the HTC Vive is extremely cool, but quite some investment for starters. Decided to get myself a decent Android phone and a Gear VR, and started porting my astronomy app Cor Leonis to Unity. Good progress so far! Stars, planets, moon, and sun are all in, reading device location and compass is a breeze in Unity, so I can already have a view of the…
-
Arduino Prototyping: It’s a clock!
Over the past few months, I digged more deeply into the Arduino platform. One ongoing project is a clock with moon phase display (since I already implemented the computations for my astronomy app, Cor Leonis). I started out with an LED matrix and 7-segment displays like this: Tons of wire! Over time, I decided to use 2 8×8 LED matrices, switched to a smaller Arduino compatible board (Adafruit Pro Trinket),…
-
Cor Leonis 5.0 released
After a looooong break, I picked up development on my astronomy app, Cor Leonis, again. The latest version 5.0 is available now for iOS devices in the Apple App Store. The one big feature which justifies the major version jump: the moon! While I was working on the moon info panel, I also beefed up information about the planets in our solar system a lot. Hope you like it!
-
Bouncing Ball Physics
To revive my Blender skills, I’ve been tinkering with setting up a simple bouncing ball animation. How do you keyframe this properly, without running a physics simulation? There are tons of tutorials on the web on basic bouncing ball demos, but few go into details about what a physically plausible bouncing ball trajectory would look like. As it turns out, with an ideal bouncing ball, there are only a few…
-
-

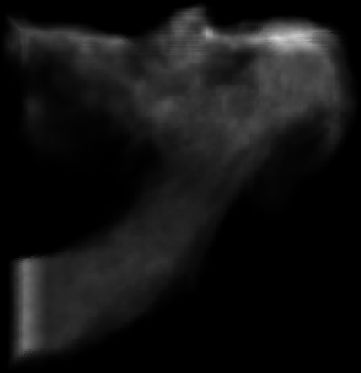
Volumes and surfaces
- Research prototype
- C++ / Qt / OpenGL / GLSL
- Volume visualization
- Geometry processing
-
Ocean water simulation
At Scanline VFX, we were doing a whole lot of CG water for the movie “Megalodon – Hai-Alarm auf Mallorca”. I leave it to you to rate the movie, but, hey: the project got me a credit on The Internet Movie Database. My part in this was the R&D on ocean water surface simulation. I ended up doing a variation of the FFT-based approach put forth by Jerry Tessendorf, and combined…
-
Facial Animation and Modeling
Facial animation is, despite all advances on the technical front, still a challenge and a rewarding research subject. This might be the one-line summary of my PhD thesis, the outcome of my time at the Max-Planck-Institut für Informatik in Saarbrücken. In a few more words, I developed an anatomy-based modeling approach in conjunction with a physically-based animation system. The title of my thesis is “A Head Model with Anatomical Structure…
